Migration & Demographics
Bachelor's Thesis analyzing the statistical impact of international migration flows on the demographic structure of Italian provinces.
Demographic dynamics are driven by natural balances (births and deaths) and migratory movements. While natural factors are endogenous determinants, migrations are complex events capable of altering the age structure and fertility potential of a territory.
This project, developed as my Bachelor’s Thesis in Statistics for Technologies and Sciences at the University of Padua, analyzes the quantitative effect of international migration on Italian demographics.
Objectives
- Define Demographic Indicators: Analyze fertility (Total Fertility Rate), birth rates, and structural indices such as the Aging Index and Dependency Ratio.
- Statistical Modeling: Apply Linear Regression (OLS) and Generalized Linear Models (GLM) to quantify the relationship between migration flows and demographic changes.
- Longitudinal Analysis: Evaluate these dynamics across 107 Italian provinces over a 15-year period (2004-2018).
My role
- Data curation and cleaning using ISTAT (Italian National Institute of Statistics) public data.
- Reconstruction of historical series accounting for administrative boundary changes and provincial reforms.
- Implementation of OLS, GLM (Gamma), and “First Difference” models in R.
- Interpretation of results considering socio-economic confounders like Unemployment and Regional GDP.
Tech Stack
| Language | R |
|---|---|
| Models | OLS, GLM |
| Data Source | ISTAT, AIRE |
| Scope | Time Series, Panel Data Analysis |
Project Phases
The research follows a rigorous statistical workflow:
01_indicatorsDefinition of fertility (TFR) and structural indices02_exploratoryEDA, normality tests, and historical context03_modelingImplementation of OLS and GLM Gamma models04_validationComparison via AIC and R-squared metrics
The Context: Italy’s Demographic Shift
The analysis focused on the period between 2004 and 2018, a timeframe marked by the 2008 global economic crisis which significantly altered migratory patterns. The study utilized a dataset of 1,498 observations (107 provinces over 14 years).
Historical data revealed that emigration flows more than tripled during this period, rising from roughly 50,000 to over 156,000 annual departures. Immigration, while more consistent in absolute numbers, showed high volatility peaking in 2007.
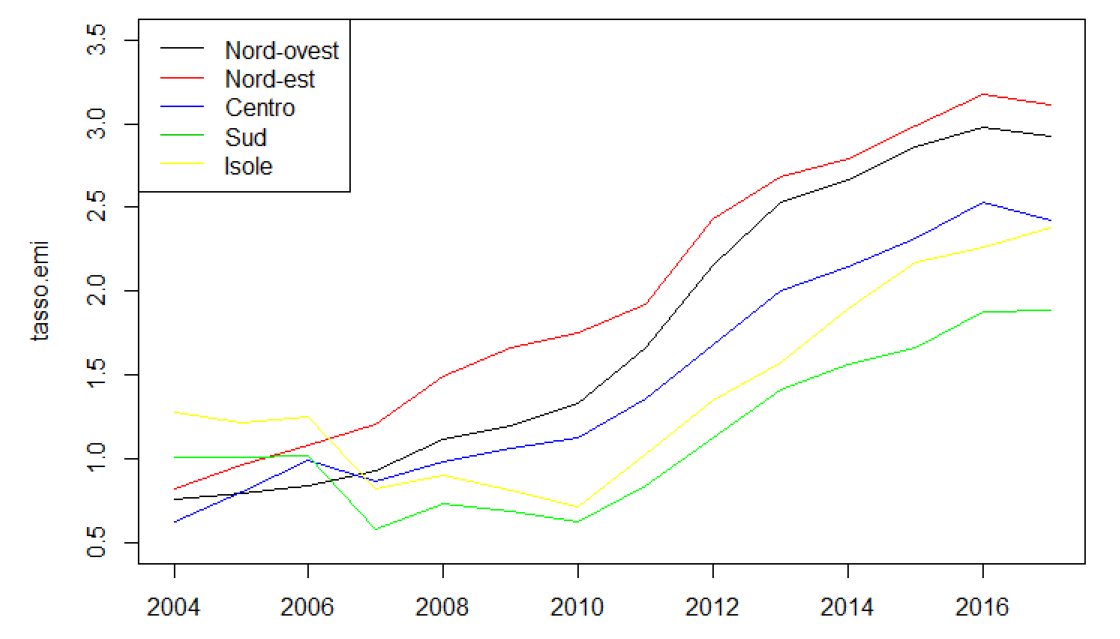
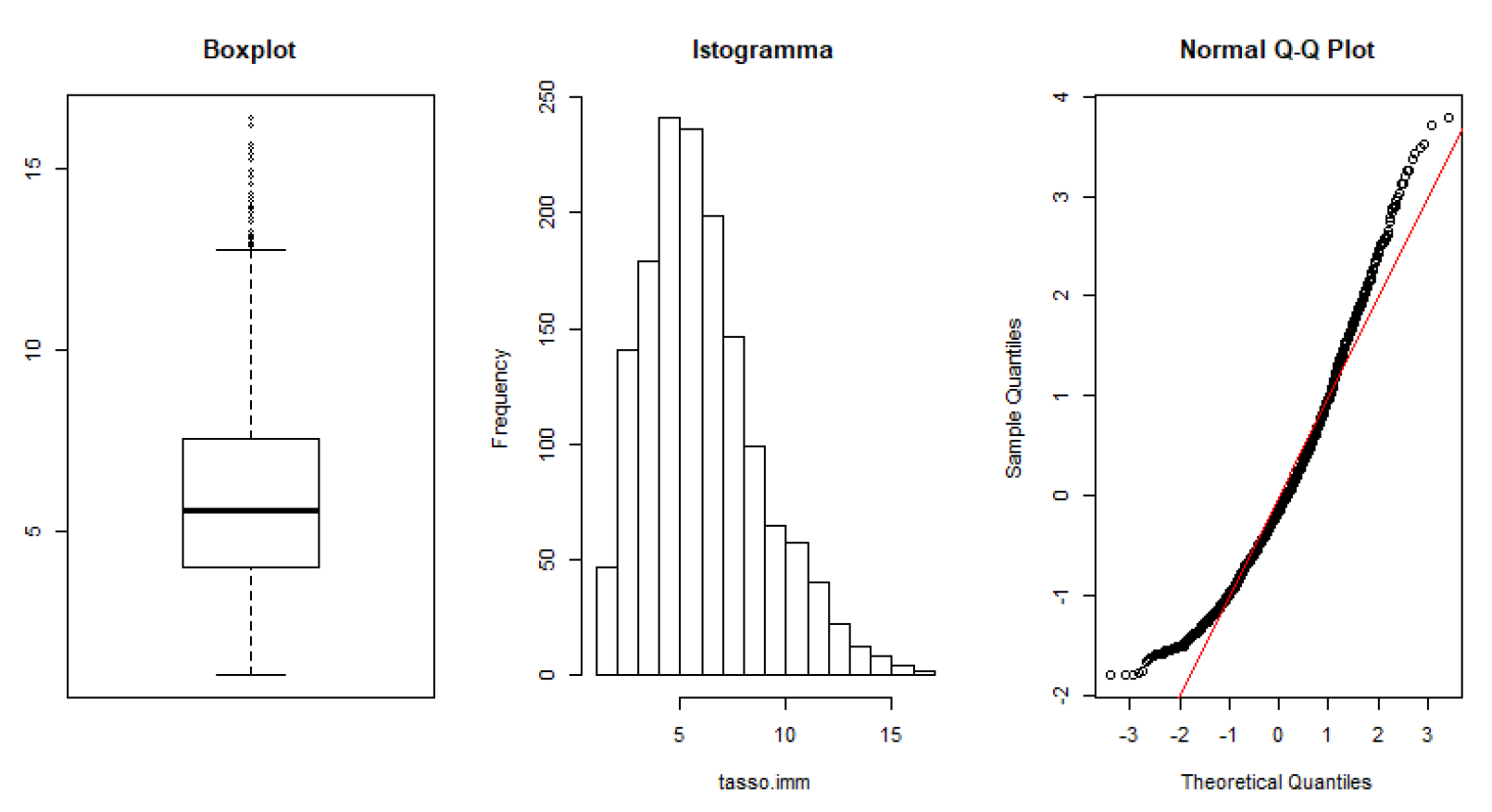
Methodology
To isolate the effect of migration from other socio-economic factors, the study employed a comparative modeling approach:
- Exploratory Data Analysis (EDA): Univariate analysis through Boxplots, Histograms, and Q-Q plots to assess data distribution and normality (Shapiro-Wilk).
- Multiple Linear Regression (OLS): Models were built to evaluate the impact of migration rates while controlling for Unemployment (push factor) and Regional GDP (pull factor).
- Generalized Linear Models (GLM): A Gamma distribution was assumed for the response variables to better fit the observed demographic data, comparing different link functions (Identity, Log, Inverse).
- First Difference Model: This approach focused on the variation between consecutive years to capture immediate dynamic changes in demographic indicators.
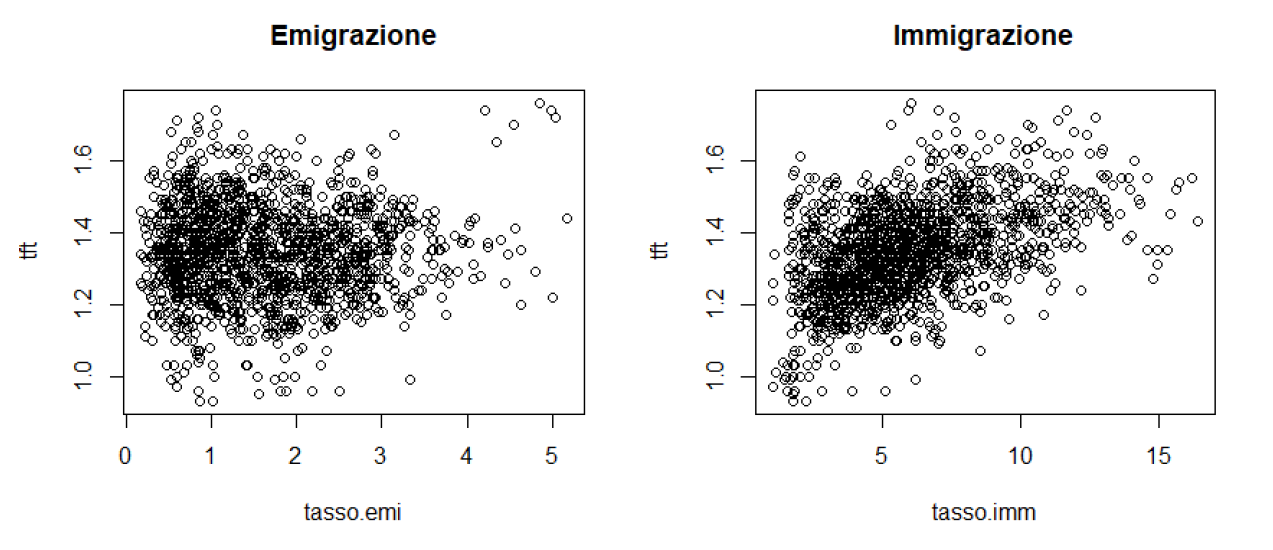
Results: Migration as a Demographic Driver
The models provided quantitative evidence of how migration influences the demographic “vitality” of Italian provinces.
Key Findings:
- Fertility Impact: Immigration shows a strongly significant positive correlation with the Total Fertility Rate, while emigration shows a slight negative impact.
- Age Structure: Emigration contributes to the aging of the population (increasing the Average Age), whereas immigration has a complex role that varies by macro-area.
- Economic Interaction: Regional GDP acts as a resistance factor for emigration and an attraction factor for immigration, directly influencing provincial birth rates.
- Model Fit: In almost all cases, GLM models outperformed standard OLS according to the Akaike Information Criterion (AIC), suggesting that demographic indicators are better represented by a Gamma distribution.
Full Documentation
For a detailed look at the mathematical derivations and the complete provincial dataset, you can access the full thesis below:
Read Full Thesis