Real Estate Forecasting
Master's Thesis on comparative analysis between Spatial Econometrics and Machine Learning models for housing price prediction.
Real estate valuation is a complex task where location introduces strong spatial dependencies that standard models often fail to capture. This project, developed as my Master’s Thesis in Statistical Sciences, explores the intersection of classical Spatial Econometrics and modern Machine Learning to predict housing prices in Madrid.
Objectives
- Data Engineering: Build a robust dataset by scraping and geocoding thousands of real estate listings.
- Missing Data Strategy: Compare and implement advanced imputation techniques (e.g., Random Forest vs. Predictive Mean Matching) to handle incomplete records.
- Model Benchmarking: Evaluate whether explicitly modeling spatial dependence (Spatial Error/Lag Models) outperforms algorithmic approaches (XGBoost, Random Forest).
My role
- End-to-end data pipeline development (Web Scraping -> Cleaning -> Imputation).
- Statistical analysis of spatial autocorrelation (Moran’s I, LISA Clusters).
- Implementation and tuning of predictive models.
- Comparative analysis of error metrics (RMSE, MAE).
Tech Stack
| Language | R |
|---|---|
| Spatial Stats | spdep, spatialreg, sf, tmap |
| ML Models | xgboost, randomForest, caret |
| Tools | ArcGIS (Geocoding), OpenStreetMap |
Project Structure
The workflow follows a rigorous statistical framework:
01_data_collectionScraping & Geocoding02_imputationMissing data handling (I-Score)03_spatial_esdaMoran's I & LISA Clustering04_modelingSEM/SAR vs XGBoost/RF
The Challenge: Spatial Dependence & Data Quality
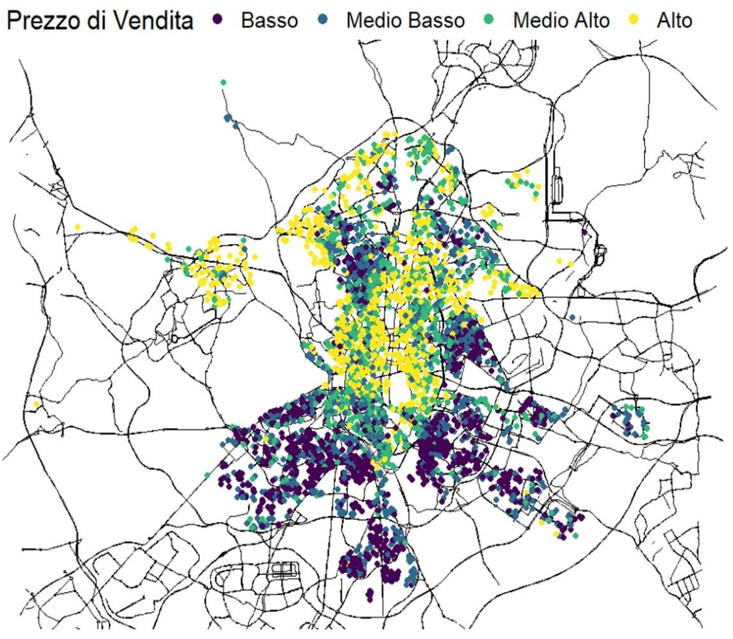
The dataset consists of 6,287 properties in Madrid, collected in March 2020. Real-world data is rarely perfect: significant portions of the data (up to 48% for some variables like “Independent Heating”) were missing.
Furthermore, housing prices violate the assumption of independence required by standard linear models: the price of a house is strongly correlated with the price of its neighbors (Spatial Autocorrelation).
Key Challenges:
- Missing Data (MAR): Analyzing the mechanism of missingness (Missing At Random) to apply the correct imputation strategy without introducing bias.
- Spatial Heterogeneity: The relationship between variables changes across different neighborhoods (spatial sub-markets).
Methodology
The analysis adopted a hybrid approach, testing both “Explicit” and “Implicit” spatial modeling:
- Data Preprocessing & Imputation: Comparing multiple imputation methods using the I-Score metric. Random Forest Imputation proved to be the most effective at preserving the original data distribution.
- Spatial Analysis (ESDA): Using Global Moran’s I to detect autocorrelation and LISA (Local Indicators of Spatial Association) to identify “hotspots” (High-High price clusters) and “coldspots” (Low-Low clusters).
- Modeling Strategies:
- Spatial Econometrics: Spatial Error Model (SEM) and Spatial Lag Model (SAR) to explicitly model the error structure or the dependent variable lag.
- Machine Learning: Random Forest and XGBoost.
- Hybrid Approach: Using spatial features (LISA Cluster IDs) as input features for tree-based models (“Implicit Spatial Regression”).
Results: The Power of Context
The results highlighted a trade-off between explainability and predictive power.
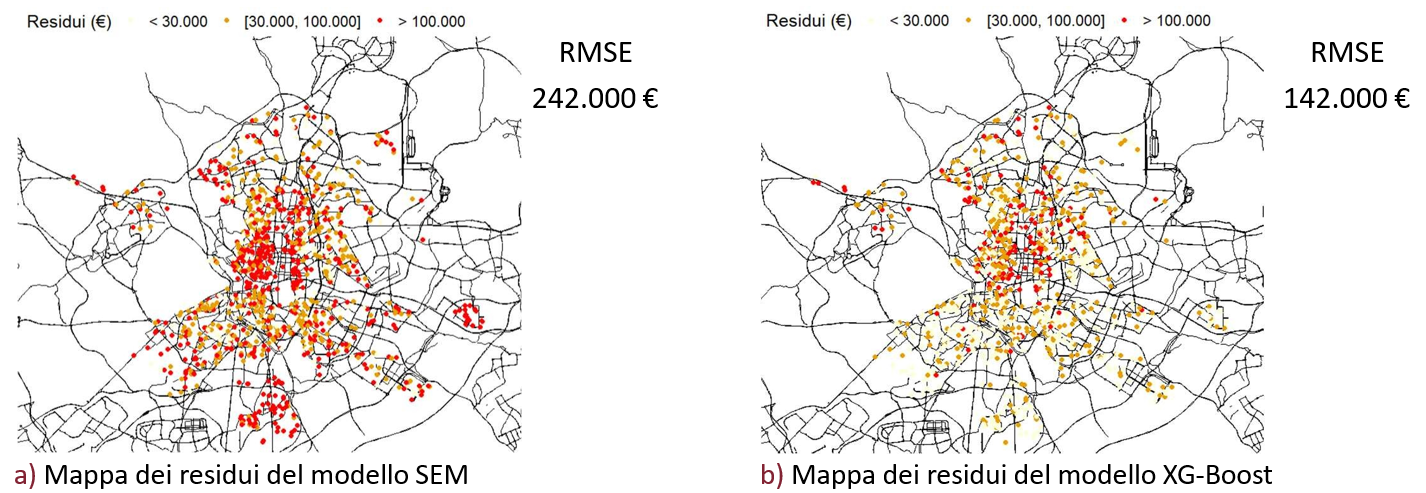
While Spatial Econometrics models (SEM) provided excellent theoretical insights into the spatial structure of the errors, they underperformed in pure prediction accuracy compared to ensemble methods.
Key Findings:
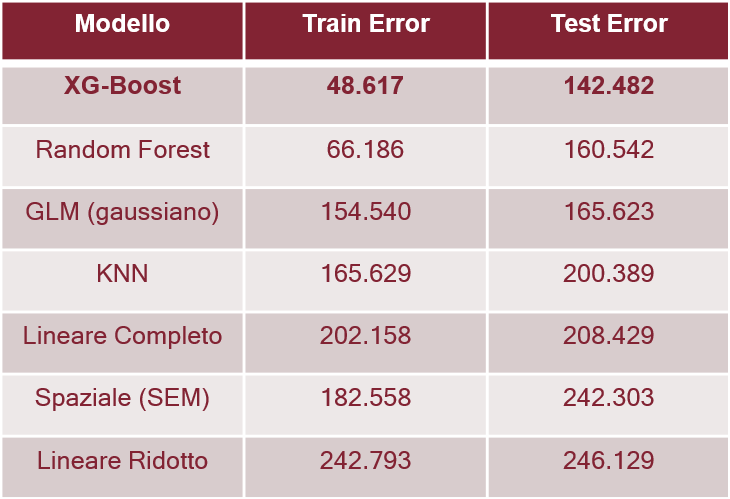
- XGBoost outperformed all traditional statistical models.
- The Hybrid Winner: The best performance was achieved by an XGBoost model enriched with spatial features (LISA cluster IDs). This approach captured local spatial heterogeneity better than global spatial parameters.
Performance Metrics (RMSE):
- Spatial Error Model (SEM): ~242,000 €
- Linear Regression: ~208,000 €
- XGBoost (Hybrid): ~142,000 €
The hybrid model explained 89.9% of the variance in housing prices, reducing the average error significantly compared to traditional methods.
Full Documentation
For a deep dive into the mathematical formulation of the Spatial Error Models and the complete variable analysis, you can access the full documents below:
Read Full Thesis View Presentation Slides